Ο Θαλής ο Μιλήσιος, (640 ή 624 π.Χ. - 546 π.Χ.)

Ο Θαλής ο Μιλήσιος, (640 ή 624 π.Χ. - 546 π.Χ.) είναι ο αρχαιότερος προσωκρατικός φιλόσοφος, ο πρώτος των επτά σοφών της αρχαιότητας, μαθηματικός, φυσικός, αστρονόμος, μηχανικός, μετεωρολόγος και ιδρυτής της Ιωνικής Σχολής της φυσικής φιλοσοφίας στη Μίλητο. 

Κυρίως ο Αριστοτέλης, αλλά και άλλοι αρχαίοι φιλόσοφοι θεωρούν τον Θαλή ως τον πρώτο Έλληνα φιλόσοφο.Στον διάλογο του Πλάτωνα Πρωταγόρας, το όνομα που εμφανίζεται πρώτο στην λίστα πεπαιδευμένων ανθρώπων είναι του Θαλή του Μιλήσιου. Χαρακτηριστικά ο Μπέρτραντ Ράσελ είπε πως «Η Δυτική φιλοσοφία αρχίζει με τον Θαλή» 

Ο Θαλής προσπάθησε να κατανοήσει τον κόσμο μέσα από τα μάτια της επιστήμης και να εξηγήσει φυσικά φαινόμενα όπως λ.χ την Έκλειψη Ηλίου, χωρίς να χρησιμοποιεί αναφορές στην μυθολογία, όπως γινόταν μέχρι την εποχή του. Υπήρξε μεγάλος διδάσκαλος με παρά πολύ μεγάλη επιρροή σε όλους σχεδόν τους μεταγενέστερους προσωκρατικούς φιλοσόφους. Αυτοί ακολούθησαν τα χνάρια του στην προσπάθειά τους να δημιουργήσουν τεκμηριωμένες αδιαμφισβήτητες αληθείς πεποιθήσεις για τα φυσικά φαινόμενα, τα ουράνια σώματα, και άλλα χρησιμοποιώντας ως εργαλεία τους την Λογική, τα μαθηματικά, την φυσική, τη βιολογία, την αστρολογία και όχι τους μύθους και τους θρύλους. 

Αυτοί οι φιλόσοφοι, με πρωτοπόρο τον Θαλή τον Μιλήσιο, απέρριψαν όλες τις μυθολογικές εξηγήσεις των φυσικών φαινομένων (όπως λ.χ. το μύθο της αρπαγής της Περσεφόνης ως ερμηνεία της εναλλαγής των εποχών ή τη γνωστή αναφορά του Αρχίλοχου) και χάρη στο θεμέλιο λίθο που έθεσε η δική τους θεώρηση των πραγμάτων, η ανθρωπότητα άρχισε να αναζητά την αλήθεια μακριά από θρησκευτικές πεποιθήσεις, ανοίγοντας τον δρόμο στην πρωτόγονη μεν, επιστημονική έρευνα δε.

Τη βιογραφία του Θαλή έγραψε ο Διογένης ο Λαέρτιος.

Γεωμετρία

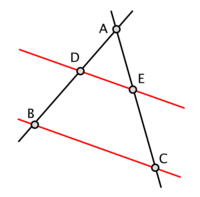
Το Θεώρημα του Θαλή. Για το παραπάνω σχήμα ισχύει: ${\displaystyle \textstyle {\frac {DE}{BC}}={\frac {AE}{AC}}={\frac {AD}{AB}}}$

Ο Θαλής αναφέρεται ως σπουδαίος γεωμέτρης. Κέρδισε μάλιστα τον θαυμασμό των Αιγυπτίων μετρώντας το ύψος των πυραμίδων, βασιζόμενος στο μήκος της σκιάς τους και της σκιάς μιας ράβδου που έμπηγε στο έδαφος.

Γνωστό είναι το Θεώρημα του Θαλή που αναφέρει: όταν παράλληλες ευθείες τέμνονται από δύο άλλες ευθείες τότε τα τμήματα μεταξύ των παραλλήλων που ορίζονται στην μια τέμνουσα, είναι ανάλογα ……

Στον Θαλή αποδίδονται από τους αρχαίους συγγραφείς πέντε ακόμα αποδείξεις γεωμετρικών προτάσεων που είναι οι ακόλουθες

1. Η διάμετρος κύκλου διχοτομεί τον κύκλο.
2. Οι κατά κορυφήν γωνίες είναι ίσες.
3. Οι παρά τη βάση ισοσκελούς τριγώνου γωνίες είναι ίσες.
4. Αν δυο τρίγωνα έχουν μια πλευρά ίση και τις προσκείμενες σε αυτή γωνίες ίσες, είναι και μεταξύ τους ίσα (Κριτήριο Γ-Π-Γ).
5. Η εγγεγραμμένη σε ημιπεριφέρεια γωνία είναι ορθή.