Pythagorean triples

Pythagorean triples

Main article: Pythagorean triple

A Pythagorean triple has three positive integers a, b, and c, such that a² + b² = c². In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths.Such a triple is commonly written (a, b, c). Some well-known examples are (3, 4, 5) and (5, 12, 13).

A primitive Pythagorean triple is one in which a, b and c are coprime (the greatest common divisor of a, b and c is 1).

The following is a list of primitive Pythagorean triples with values less than 100:

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)

 

Incommensurable lengths

 

The spiral of Theodorus: A construction for line segments with lengths whose ratios are the square root of a positive integer

One of the consequences of the Pythagorean theorem is that line segments whose lengths are incommensurable (so the ratio of which is not a rational number) can be constructed using a straightedge and compass. Pythagoras's theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides by the square root operation.

The figure on the right shows how to construct line segments whose lengths are in the ratio of the square root of any positive integer. Each triangle has a side (labeled "1") that is the chosen unit for measurement. In each right triangle, Pythagoras's theorem establishes the length of the hypotenuse in terms of this unit. If a hypotenuse is related to the unit by the square root of a positive integer that is not a perfect square, it is a realization of a length incommensurable with the unit, such as √2, √3, √5 . For more detail, see Quadratic irrational.

Incommensurable lengths conflicted with the Pythagorean school's concept of numbers as only whole numbers. The Pythagorean school dealt with proportions by comparison of integer multiples of a common subunit. According to one legend, Hippasus of Metapontum (ca. 470 B.C.) was drowned at sea for making known the existence of the irrational or incommensurable.

  

Complex numbers

 

The absolute value of a complex number z is the distance r from z to the origin

For any complex number

${\displaystyle z=x+iy,}$

the absolute value or modulus is given by

${\displaystyle r=|z|={\sqrt {x^{2}+y^{2}}}.}$

So the three quantities, r, x and y are related by the Pythagorean equation,

${\displaystyle r^{2}=x^{2}+y^{2}.}$

Note that r is defined to be a positive number or zero but x and y can be negative as well as positive. Geometrically r is the distance of the z from zero or the origin O in the complex plane.
This can be generalised to find the distance between two points, z₁ and z₂ say. The required distance is given by

${\displaystyle |z_{1}-z_{2}|={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}},}$

so again they are related by a version of the Pythagorean equation,

${\displaystyle |z_{1}-z_{2}|^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}.}$

 

Euclidean distance in various coordinate systems

The distance formula in Cartesian coordinates is derived from the Pythagorean theorem. If (x₁, y₁) and (x₂, y₂) are points in the plane, then the distance between them, also called the Euclidean distance, is given by

${\displaystyle {\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}.}$

More generally, in Euclidean n-space, the Euclidean distance between two points, ${\displaystyle A\,=\,(a_{1},a_{2},\dots ,a_{n})}$ and ${\displaystyle B\,=\,(b_{1},b_{2},\dots ,b_{n})}$, is defined, by generalization of the Pythagorean theorem, as:

${\displaystyle {\sqrt {(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+\cdots +(a_{n}-b_{n})^{2}}}={\sqrt {\sum _{i=1}^{n}(a_{i}-b_{i})^{2}}}.}$

If Cartesian coordinates are not used, for example, if polar coordinates are used in two dimensions or, in more general terms, if curvilinear coordinates are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the applications of Legendre polynomials in physics. The formulas can be discovered by using Pythagoras's theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates (r, θ) can be introduced as:

${\displaystyle x=r\cos \theta ,\ y=r\sin \theta .}$

Then two points with locations (r₁, θ₁) and (r₂, θ₂) are separated by a distance s:

${\displaystyle s^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}=(r_{1}\cos \theta _{1}-r_{2}\cos \theta _{2})^{2}+(r_{1}\sin \theta _{1}-r_{2}\sin \theta _{2})^{2}.}$

Performing the squares and combining terms, the Pythagorean formula for distance in Cartesian coordinates produces the separation in polar coordinates as:

${\displaystyle {\begin{aligned}s^{2}&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\left(\cos \theta _{1}\cos \theta _{2}+\sin \theta _{1}\sin \theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \left(\theta _{1}-\theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \Delta \theta ,\end{aligned}}}$

using the trigonometric product-to-sum formulas. This formula is the law of cosines, sometimes called the generalized Pythagorean theorem. From this result, for the case where the radii to the two locations are at right angles, the enclosed angle Δθ = π/2, and the form corresponding to Pythagoras's theorem is regained: ${\displaystyle s^{2}=r_{1}^{2}+r_{2}^{2}.}$ The Pythagorean theorem, valid for right triangles, therefore is a special case of the more general law of cosines, valid for arbitrary triangles.

 

Pythagorean trigonometric identity

Main article: Pythagorean trigonometric identity

Similar right triangles showing sine and cosine of angle θ

In a right triangle with sides a, b and hypotenuse c, trigonometry determines the sine and cosine of the angle θ between side a and the hypotenuse as:

${\displaystyle \sin \theta ={\frac {b}{c}},\quad \cos \theta ={\frac {a}{c}}.}$

From that it follows:

${\displaystyle {\cos }^{2}\theta +{\sin }^{2}\theta ={\frac {a^{2}+b^{2}}{c^{2}}}=1,}$

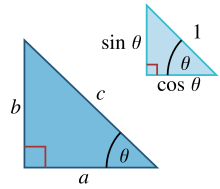
where the last step applies Pythagoras's theorem. This relation between sine and cosine is sometimes called the fundamental Pythagorean trigonometric identity. In similar triangles, the ratios of the sides are the same regardless of the size of the triangles, and depend upon the angles. Consequently, in the figure, the triangle with hypotenuse of unit size has opposite side of size sin θ and adjacent side of size cos θ in units of the hypotenuse.

 

Relation to the cross product

 

The area of a parallelogram as a cross product; vectors a and b identify a plane and a × b is normal to this plane.

The Pythagorean theorem relates the cross product and dot product in a similar way:

${\displaystyle \|\mathbf {a} \times \mathbf {b} \|^{2}+(\mathbf {a} \cdot \mathbf {b} )^{2}=\|\mathbf {a} \|^{2}\|\mathbf {b} \|^{2}.}$

This can be seen from the definitions of the cross product and dot product, as

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} &=ab\mathbf {n} \sin {\theta }\\\mathbf {a} \cdot \mathbf {b} &=ab\cos {\theta },\end{aligned}}}$

with n a unit vector normal to both a and b. The relationship follows from these definitions and the Pythagorean trigonometric identity.
This can also be used to define the cross product. By rearranging the following equation is obtained

${\displaystyle \|\mathbf {a} \times \mathbf {b} \|^{2}=\|\mathbf {a} \|^{2}\|\mathbf {b} \|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.}$

This can be considered as a condition on the cross product and so part of its definition, for example in seven dimensions.

 Generalizations

 Similar figures on the three sides

A generalization of the Pythagorean theorem extending beyond the areas of squares on the three sides to similar figures was known by Hippocrates of Chios in the 5th century BC,and was included by Euclid in his Elements:

If one erects similar figures (see Euclidean geometry) with corresponding sides on the sides of a right triangle, then the sum of the areas of the ones on the two smaller sides equals the area of the one on the larger side.

This extension assumes that the sides of the original triangle are the corresponding sides of the three congruent figures (so the common ratios of sides between the similar figures are a:b:c). While Euclid's proof only applied to convex polygons, the theorem also applies to concave polygons and even to similar figures that have curved boundaries (but still with part of a figure's boundary being the side of the original triangle).

The basic idea behind this generalization is that the area of a plane figure is proportional to the square of any linear dimension, and in particular is proportional to the square of the length of any side. Thus, if similar figures with areas A, B and C are erected on sides with corresponding lengths a, b and c then:

${\displaystyle {\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,,}$

${\displaystyle \Rightarrow A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C\,.}$

But, by the Pythagorean theorem, a² + b² = c², so A + B = C.

Conversely, if we can prove that A + B = C for three similar figures without using the Pythagorean theorem, then we can work backwards to construct a proof of the theorem. For example, the starting center triangle can be replicated and used as a triangle C on its hypotenuse, and two similar right triangles (A and B ) constructed on the other two sides, formed by dividing the central triangle by its altitude. The sum of the areas of the two smaller triangles therefore is that of the third, thus A + B = C and reversing the above logic leads to the Pythagorean theorem a² + b² = c². See #Einstein's proof by dissection without rearrangement

https://en.wikipedia.org/wiki/Pythagorean_theorem