Let acute-angled triangle  , and let
, and let 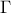 be the circumscribed circle. Points
be the circumscribed circle. Points  and
and 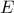 in the parts
in the parts  and
and  corresponding order
corresponding order  .
.
The perpendicular bisector of and
and  intersecting the small arches
intersecting the small arches  and
and  the
the 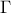 in points
in points  and
and  respectively.
respectively.
Prove that the lines and
and  are either parallel or are identical.
are either parallel or are identical.
Suppose that intersects the circumscribed circle of
intersects the circumscribed circle of  a point
a point  .
.
We observe that .
.
Thus the triangle is isosceles with
is isosceles with  .
.
Similarly if intersects circumcircle of
intersects circumcircle of  at
at  , then
, then  .
.
We will prove that , ie
, ie  .
.
We note that , while
, while  (
(  is the core of
is the core of  the circle with center
the circle with center 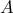 and radius
and radius  .
.
So it suffices to prove that , that
, that  .
.
But we know that , by definition
, by definition  .
.
So long .
.
We observe that the quadrilateral is recordable and
is recordable and  therefore the
therefore the  is the bisector
is the bisector 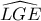 .
.
If it was not equilateral, then since
was not equilateral, then since 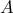 it belongs to the bisector
it belongs to the bisector 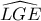 and
and  , should it
, should it  be writable (south pole theorem) inappropriate, since the circumscribed circle
be writable (south pole theorem) inappropriate, since the circumscribed circle  is the circumscribed circle
is the circumscribed circle  and
and 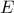 does not belong to this circle.
does not belong to this circle.
So it is isosceles with
is isosceles with  and the requested follow.
and the requested follow.
 , and let
, and let 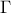 be the circumscribed circle. Points
be the circumscribed circle. Points  and
and 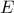 in the parts
in the parts  and
and  corresponding order
corresponding order  .
. The perpendicular bisector of
 and
and  intersecting the small arches
intersecting the small arches  and
and  the
the 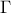 in points
in points  and
and  respectively.
respectively. Prove that the lines
 and
and  are either parallel or are identical.
are either parallel or are identical.
Solution
Suppose that
 intersects the circumscribed circle of
intersects the circumscribed circle of  a point
a point  .
. We observe that
 .
. Thus the triangle
 is isosceles with
is isosceles with  .
. Similarly if
 intersects circumcircle of
intersects circumcircle of  at
at  , then
, then  .
. We will prove that
 , ie
, ie  .
. We note that
 , while
, while  (
(  is the core of
is the core of  the circle with center
the circle with center 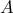 and radius
and radius  .
. So it suffices to prove that
 , that
, that  .
. But we know that
 , by definition
, by definition  .
. So long
 .
.We observe that the quadrilateral
 is recordable and
is recordable and  therefore the
therefore the  is the bisector
is the bisector 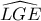 .
. If it
 was not equilateral, then since
was not equilateral, then since 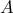 it belongs to the bisector
it belongs to the bisector 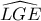 and
and  , should it
, should it  be writable (south pole theorem) inappropriate, since the circumscribed circle
be writable (south pole theorem) inappropriate, since the circumscribed circle  is the circumscribed circle
is the circumscribed circle  and
and 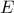 does not belong to this circle.
does not belong to this circle. So it
 is isosceles with
is isosceles with  and the requested follow.
and the requested follow.
No comments:
Post a Comment